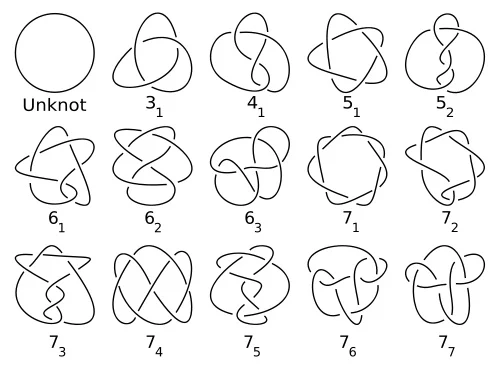
Knot theory has a rich and interesting history. The original purpose was to distinguish knots which cannot be transformed to each other by continuous transformations. The most famous example of knot polynomials is the Jones polynomial, discovered in 1984, which can be computed using the relation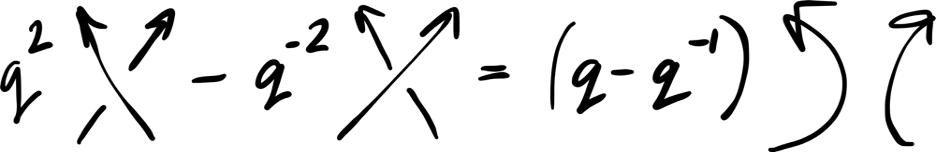
Although Jones polynomial is a very powerful knot invariant, there are many inequivalent knots with the same Jones polynomials.
There have been developed generalizations of the Jones polynomial such as HOMFLY polynomial and conjectural super-polynomials. They are at the intersection of several modern areas of mathematics such as low-dimensional topology, special functions, combinatorics, and integrable systems. In the semilab we will discuss the theory and do some computations.
Prerequisites: linear algebra