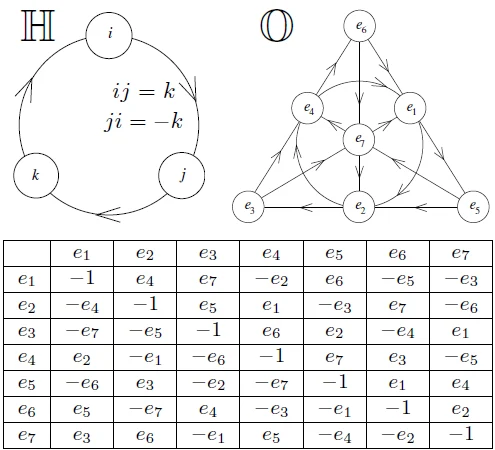
When you say "number", most people immediately think "real number". Some of you might also be familiar with complex numbers. But why these are the only kinds of numbers we ever consider? And do we really know what real numbers are - how many of you can give a definition of real numbers?
In this semilab, we will trace the history of how, starting with natural numbers, we construct more and more advanced kinds of numbers - rational, real, complex - and then go beyond this, showing you quaternions and octonions, matrices and p-adic numbers. You will learn about why there is no 3-dimensional analog of complex numbers and how it is related to hairy ball theorem, about skew-symmetric numbers and why it is related to supersymmetry in Quantum Field Theory, and more.
This is an advanced course intended for students with an interest in math. High school algebra (in particular, complex numbers and polynomials) is required. Familiarity with calculus can be useful but is not required.