What is the subject of mathematics? One of classical answers was used as the title of a book: ``Numbers and figures''. But there is another answer: not separate numbers and figures, but their sequences. For example, consider these sequences:
- 1, 2, 3, 4, 5, 6,....
- 2, 8, 18, 32, 50,....
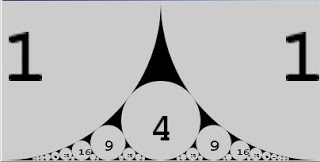

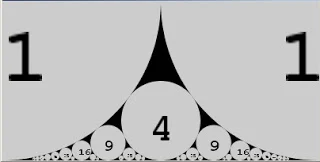
The first sequence needs no comment; the second one consists of lengths of periods in the periodic table of chemical elements; the third shows so-called Farey circles; the last is the Sierpinski gasket.
Many other remarkable sequences arise in Nature and are studied in mathematics. There is the widely cited ``On-Line Encyclopedia of Integer Sequences'', where the author collects the information on integer sequences of interest to both professional mathematicians and amateurs. In our semilab we describe some remarkable sequences and explain how mathematicians discover their patterns.