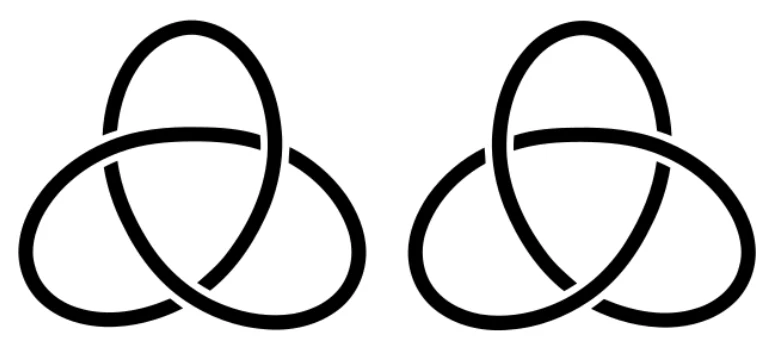
There is an old joke that a topologist is someone for whom the coffee mug looks the same as a donut. But can you explain in what way the coffee mug looks the same as a donut? Or in what way the two knots (shown here on the right) are the same - or are they the same?
In this semilab, we will explore what exactly it means for two shapes to be (topologically) the same, making precise the naive idea of deforming one shape into another. We will also talk about tools that can be used to tell different shapes apart - topological invariants. We will begin with simple invariants such as the winding number and then progress to more complicated ones: fundamental group, linking number of two circles, genus and Euler characteristic, quantum invariants of knots, and use these invariants to study two-dimensional surfaces and knots.
Prerequisites: Students should be familiar with the notion of a continuous function, at least at the level it is introduced in Calculus A course (rigorous epsilon-delta definition is not required).
Update: you can see the PDF version of course notes here: handout.pdf. If you want, you can also download the zip file containing the sources of that handout (LaTeX and images): handout.zip